I think there are 112 possible strokes for strict alternate picking

[Drew]

@Drew

It’s possible I just missed something or don’t understand where you’re going, though, so… Could you maybe try to explain why it matters that there are 112 possible alternate picking strokes, or I guess what you thinbk a guitarist needs to do with this information, that will help them become a better guitarist?

I guess that’s pretty fair. And, there’s also a lot of subjective utility here - just because my learning process doesn’t involve sitting down and mathematically solving for every possible permutation of alternate picking strokes, and practicing those, doesn’t mean maybe someone else couldn’t find value in going about it this way. I don’t get it, but… I suppose I don’t have to.

@joebegly

It’s gonna get nuanced if we think about the player’s preference for USX vs DSX but the above covers me even for 1nps with string skips. Again, I can’t question the math in the OP. But these 4 pickstrokes are a smaller number than 112 lol!

All that said, this seems a little more practically useful to me - I guess this was kind of how I was coming at it in the 'I think this is the most challenging alternate picking pattern on guitar" thread, where there seems to be two components to each movement - the direction you’re changing from string to string in, and the direction of the pickstroke itself.

[kgk]

I suspect that many people who think of themselves as strict alternate pickers might not be using the strokes that I commented out with a white box. The only downside of this would be a loss of generality, e.g., they’d have to go outside to use other techniques to play some music with big jumps, should that be of interest to them.

[Pepepicks66]

@kgk

who think of themselves as strict alternate pickers

so the insinuation here is that if they don’t play (at some point? at some speed?) all 112 combinations you’ve identified, they’re not really strict alternate picking?

[kgk]

@Pepepicks66

don’t play

It’s more like if they can’t play some of the combinations then they cannot use strict alternate picking to play arbitrary music, and that could be perfectly fine, as the player is always right by definition and decides what is important or unimportant to them.

[jptk]

[Fossegrim]

@jptk

I know it’s Halloween, but why exhume the corpse?

[kgk]

Do you have a specific question? If so, I’m happy to answer it.

[jptk]

The diagram. I’m finding it hard to understand what the pickstroke are in the diagram. It’s probably something simple that I’m missing.

[kgk]

You’re right, it’s really simple, so I’ll try to explain one line of it, and hopefully you’ll see how obvious it is, and how to look at the rest of them.

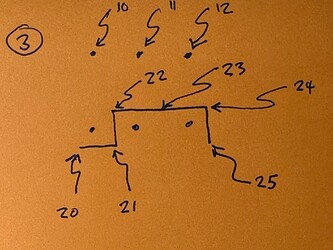
So I put some numbers down to refer to specific points. 10 is one string, 11 is another string, and 12 is the third string. I didn’t give them names because this is any three strings in a row. So, this picture will hold across EADGBE, e.g., it covers EAD, ADG, DGB, GBE, four cases.

So the pick path is represented, in the abstract, by that line. Lets’ consider it starting at 20, then going to 21, 22, 23, 24, and 25.

Big picture:

• It will start at 20, ready to hit 10.
• It will miss 11 and 12.
• It will go back down at the end, so for the NEXT STROKE it will be ready to hit 12.

So pretty much the stroke starts at 20 and ends at 25, as it goes, it hits 10, and nothing else.

The details of the path aren’t mentioned here, e.g., there might be forearm rotation to be able to move the pick from 20 to 21 to 22, and the path would likely be smoother and not so abrupt as I have drawn it, but I was interested in counting how many total strokes there actually are.

So, it starts at 20 hits 10, climbs up above 11 (or possibly swipes it for some people), goes over 12, and then that’s near the end of the stroke, as it needs to stop going in that direction; however, it definitely needs to be going back down, because the next stroke (strictly alternating) will have to hit 12.

Did this make it totally obvious (what it is), or did I add unnecessary confusion?

The main thing that made me draw these is that strictly alternate picking is a severe constraint and it really throws down the law about what is required. I really like its brutal determinism, but some of the strokes can be extremely demanding, and I had never realized that before. What people can try to do is reorganize the strings that they need to hit in order to avoid some of the really difficult strokes.

[jptk]

@kgk

Did this make it totally obvious (what it is), or did I add unnecessary confusion?

Ah! Yes now I understand it thanks.

As you mentioned, I think some of the very wide skips are very difficult and you don’t tend to see many players attempt them. Tapping and hybrid picking being “easier” alternatives for wide intervals.
I imagine it would take a significant amount of practice, experimentation, trial and error etc, to be able to figure out how to make such leaps. It’s certainly way outside of my capabilities anyway!

[familyguy1223]

Anton could probably do it

[Drew]

Is there something different signified by one set being 10-12 and the other 20-25? Or are these all unrelated arbitraty numbers?

I don’t understand the point of any of this, still… but I AM a sucker for beating dead horses and taking a concept and running with it way farther than any sane person could ever want to, so from that standpoint, right on!

[kgk]

@Drew

Or are these all unrelated arbitraty numbers?

Right, the numbers are arbitrary.

@Drew

I don’t understand the point of any of this

One claim behind strict alternate picking is that it is totally general and has no special-purpose escape hatches. For this to be true, it requires that one can play all of those strokes, where some of them are actually pretty difficult (at least for me). My guess is that most people who say they strictly alternate pick only do a subset of those strokes, and that’s all good! In fact, I didn’t even think about certain types of strokes until I tried to count them all.

[lowD]

Anyone who can play the guitar at all can play all those strokes, if they do it at 5bpm. How fast does someone need to be able to play all these strokes in order to be able to “strictly alternate pick” according to your definition?

[kgk]

I don’t define the speed, the player does. Then, once they choose their speed, if they can do all of the strokes, they can play anything… if not, they’ll need to do things like reorganize the strings, hybrid pick, etc., to work around strokes that they can’t play at speed.

[lowD]

@kgk

I don’t define the speed, the player does. Then, once they choose their speed, if they can do all of the strokes, they can play anything…

That seems unlikely. Why would you assume that just because they can play a given stroke at speed in isolation, they can play any phrase or line including that stroke?

[kgk]

If they can play all of the strokes, I presume that they can chain them together, as the boundaries are clear given the change of direction each time. But I am no expert and could certainly be wrong.

[Drew]

@kgk

Right, the numbers are arbitrary.

Wouldn’t it be easier to present this, though, if you consistently used the same arbitrary numbers?

By that I mean, using 10-11-12-13 in one example, and then 20-21-22-23-24 in another… why just start on the same number for all examples? Starting with 1 would be the most logical, but there’s no reason you couldn’t start at 10, I suppose… It just creates this impression that there’s something else going on, beyond “this is your first stroke, then your second, then your third…”

[kgk]

That was an example of a single stroke, not multiple strokes. I labeled it in accordance with a very common recipe that is used in patents, but perhaps there are better ways to annotate it, I don’t know.

[Fossegrim]

I wouldn’t do that for this. It just obscures the concept. Pick a consistent series and stick with it.