Firstly, let me say I have no idea if this will be helpful to anybody. This is just abstract nonsense. I like abstract nonsense.
Hopefully, it might at least be interesting.
Let me first explain my motivations. When I started learning scale patterns on guitar, I found it difficult to immediately recognize the scale degree of each note in the patterns. As a direct result of this, I found it difficult to build chord shapes from these patterns. I eventually managed to learn and memorize this via repetition, but I always felt that method was inefficient.
Later, when I was learning patterns for other diatonic scales, so I could follow chord changes, I again had difficulty recognizing scale degrees, thus making it difficult to visualize the strong notes to target. At that time, I had an idea, which I’ve followed down the rabbit hole, and which I hope to explain here in this thread.
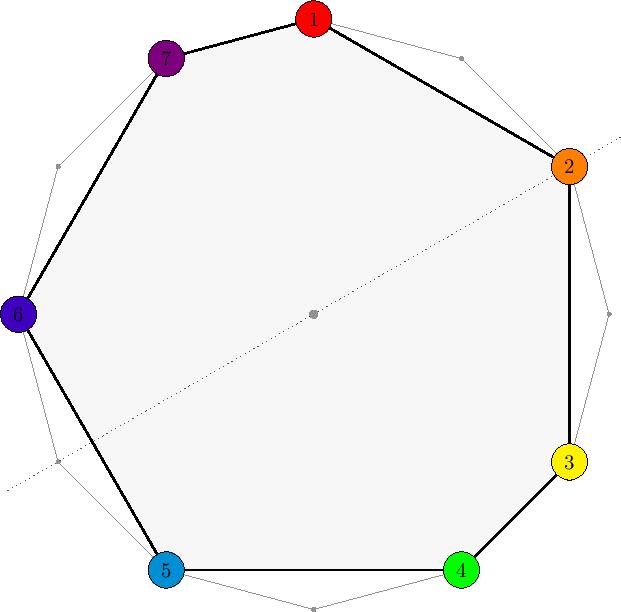
I visualize the octave as a set of 12 inequivalent pitch classes (“notes”) with a regular arrangement. Due to the regularity of this arrangement (by equal temperament), I naturally represent the octave as a regular 12-gon.
I now visualize the major scale as a 7-note subset of this 12-note set, arranged as a polygon within the regular 12-gon. See this diagram.
To distinguish scale degrees, I assign a “scale spectrum” to each inequivalent 7-note scale. For the major scale, the natural choice was the spectrum below.

I see scales as equivalent if they produce the same 7-sided polygon (that is, they contain the same arrangement of intervals). Thus, the modes of the major scale are equivalent to the major scale itself.
Notice that the 7-sided polygon clearly indicates that the major scale is reflectively symmetric through its 2nd degree. Actually, rotations and reflections of the 12-gon results in the same 7-sided polygon. This is the foundation of how I view modulations.
Now, I needed a method to visualize the chords determined by this scale. To me,chord, consisting of three notes, a seventh, and any characteristic additions. Visually, I represent the 7 chords as “chord flags,” which I’ve included below.
To read a flag, notice first the tricolour. From left to right, the colours of the tricolour indicate the root, 3rd and 5th. The interval between each chord tone is represented by the direction of the indentations in the tricolour. Notice that chord quality of the chord (major, minor, minor with flattened 5th) is then given a distinctive arrangement of the tricolour indentations.
The large central emblem represents the 7th, and is thus a 7-pointed star for a major 7th or regular heptagon for a minor 7th. If there is a shape contained within the central emblem, it indicates a characteristic addition. For the major scale, these are as follows
- The 2 chord has a major 6th, represented by a 6-pointed star.
- The 3 chord has a minor 2nd, indicated by the rectangle.
- The 4 chord has a sharped 4th, indicated by the diamond (a 4-pointed star).
- The 7 chord has a minor 2nd, indicated by the rectangle.
The 1, 5 and 6 chords are archetypal, representing standard major, dominant 7th and minor 7th chords.
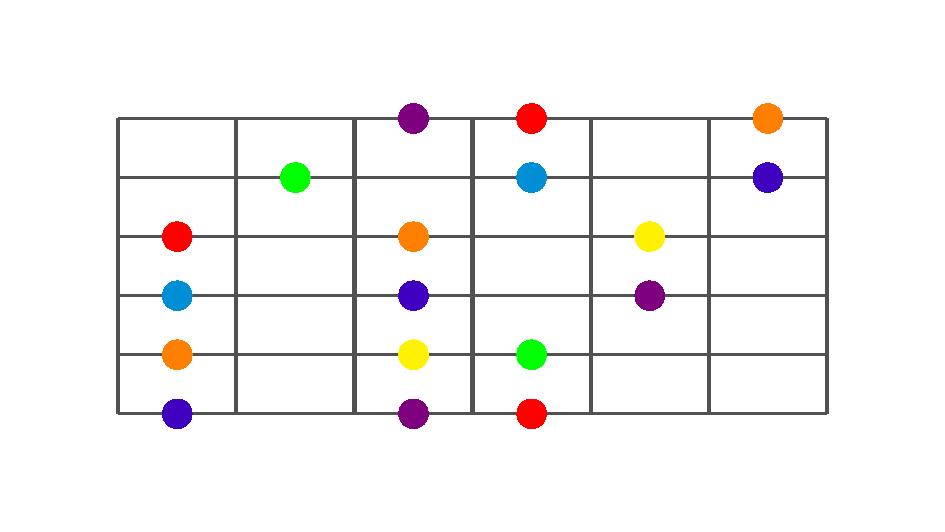
Ok, now we apply this to the guitar via scale shapes. Since I don’t see modes as different scales, I decided to use the usual mode names to denote scale shapes. This helps me to visualize the patterns of other diatonic scales (harmonic major, harmonic minor, melodic minor) as alterations of major scale shapes.
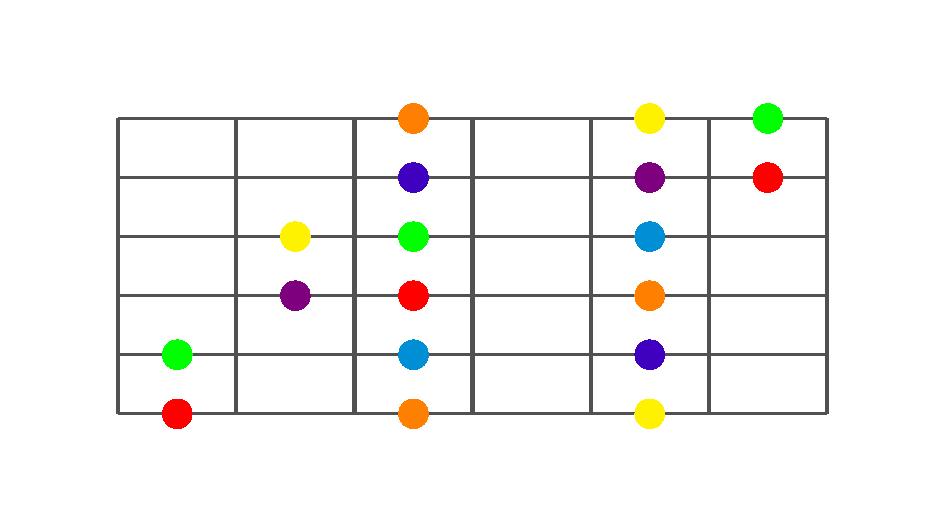
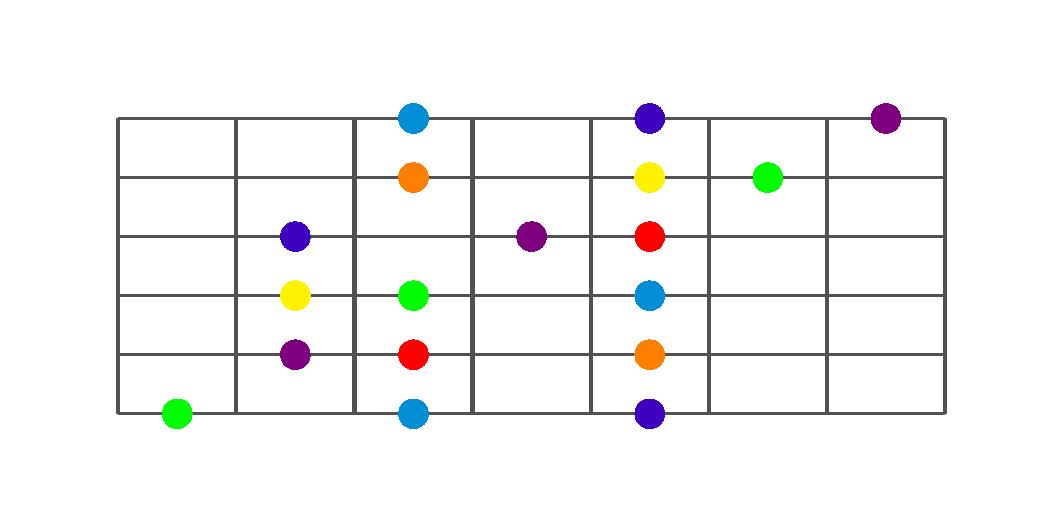
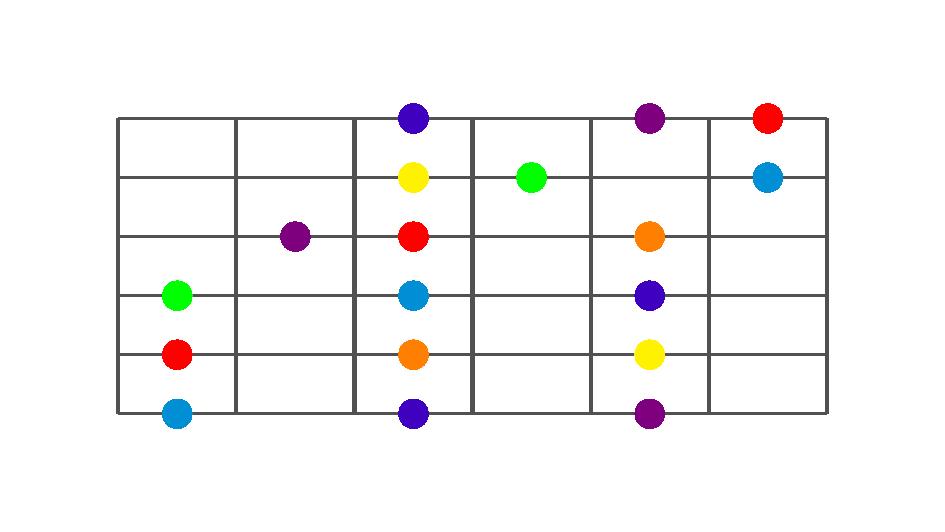
We then apply the spectrum to the usual three note per string scale shapes, and we have the following fretboard diagrams.
-
Ionian
-
Dorian
-
Phrygian
-
Lydian
-
Mixolydian
-
Aeolian
-
Locian
Now, with the scale spectrum applied to the scale patterns, it is easy to recognize the scale degrees and thus build chords and target the notes which define the chord.
I’ve repeated this idea for the other main inequivalent scales, allowing me to better see how the patterns intersect and how the chord structures change.
Let me know if this is interesting to you, and maybe I’ll develop this further in later posts.











 I think a lot of useful discoveries and explanations start out that way.
I think a lot of useful discoveries and explanations start out that way.