Calculating the angle to escape being trapped

[kgk]

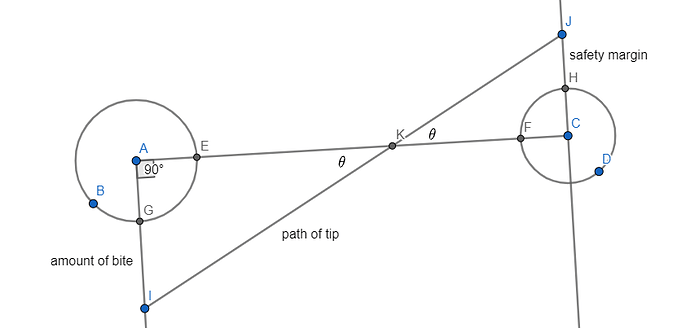
I was imagining a trapped pick that was about to escape where the strings have a nearest spacing of T. (Let’s make all of the units be in millimeters, so T=10.5mm or so.) If the pick hits a distance R away from its tip on the string that it is trapped by (say R=3mm) and clears the next string by r as a safety margin (say r=3mm), what is the angle? I think it is 35 degrees.

It seems that the answer (hopefully I did it right!) is a simple formula,

angle = arcsin((R + r) / T).

So notice that the formula doesn’t care what’s R and what’s r, it just adds them up!

So, I can just make a little table of R + r and the angle, where the first column is the total mm of radius, and the second column is the resulting angle in degrees. I suspect that normal people would have a lot of trouble going much below 6mm.

0: 0
1: 6
2: 11
3: 17
4: 23
5: 29
6: 35
7: 42
8: 50
9: 59
10: 73

So why is this interesting? It suggests that if one hits with a lot of pick and has a big safety margin then the angle has to be steep. But it also explains why reciprocating while trapped on a single string might make sense, as there are two convenient nearby exit options (as has been pointed out by @joebegly, @Riffdiculous and surely some others).

Here is a picture so other people can work out the geometry and correct my mistake if I made one, so I can fix the numbers here to be correct. (Rather than “angle of tip,” I wish that I wrote, “path of tip.”)

[Prlgmnr]

heehee it looks like it says “shits”

[MichaelT]

The formula that you arrived at is correct as long as we assume that the radius of the string is negligible. The assumption of 3mm as a safety margin seems to me to be somewhat arbitrary. This is a very important number, mathematically equal in importance to the amount of bite in terms of the escape angle, though it does not contribute to the actual sound and is therefore less important than the amount of bite.

The drawing that you made seems to imply that the point at which the pick crosses the plane of the strings must be the midpoint of T, but this is not necessarily going to be the case. It’s possible for that point (K in my diagram) to be anywhere between the strings, so that a big bite could also have a shallow escape angle, but this would necessitate a small safety margin and a crossing point K close to the next string.

I wonder what the consequences of this are for the Paul Gilbert lick, that is, what is I’m alternate picking primarily on the low string in the diagram and need to hit a single note on the higher string before returning to the lower one. To do this I am going to need to alter the path of the tip. Should I be aiming for a reflection of the original path of the tip, which would reverse my safety margin and bite for those 2 strokes before I return to my original path?